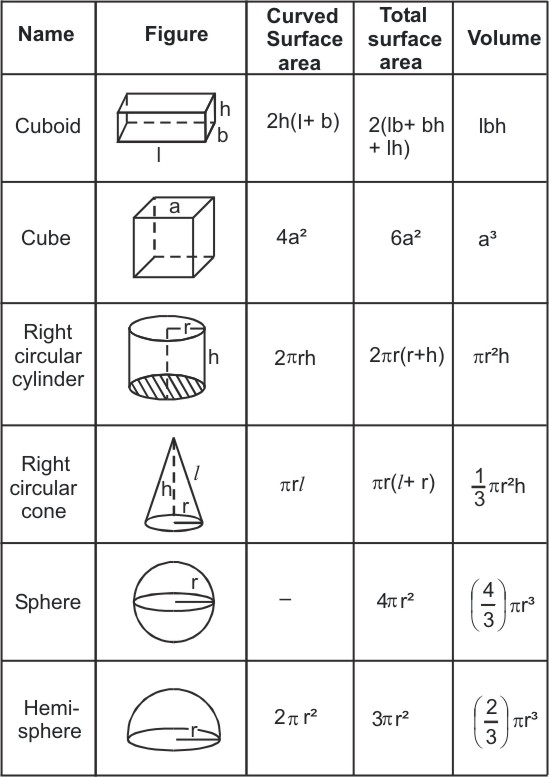
3 Dimensional Figures:
Three dimensional figures have volumes as they have all the three dimensions height, breadth, length. If you observe carefully, the base of a 3-dimensional figure is a 2-dimensional figure. If you multiply the area of the base with height, you get the volume. Area for three dimensional figures is called surface area. It is simply summation of the areas of several 2 dimensional figures on the 3 dimensional figures.

Three dimensional figures have volumes as they have all the three dimensions height, breadth, length. If you observe carefully, the base of a 3-dimensional figure is a 2-dimensional figure. If you multiply the area of the base with height, you get the volume. Area for three dimensional figures is called surface area. It is simply summation of the areas of several 2 dimensional figures on the 3 dimensional figures.
1. Find the curved surface area of a hemisphere whose diameter is 14 cm.
Radius of hemisphere = $\displaystyle\frac{1}{2}$ x 14 cm = 7 cm.
Therefore, Curved surface Area = $2\pi r^2 $ = 2 x $\displaystyle\frac{{22}}{7}$ x 7 x 7 = 308 ${\rm{cm}}^{\rm{2}} $
2. Find the height of a cuboid whose volume and base area are 144 ${\rm{m}}^{\rm{3}} $ and 18 ${\rm{m}}^{\rm{2}} $ respectively.
Height of the cuboid = $\displaystyle\frac{{{\rm{Volume}}}}{{{\rm{Base Area}}}}$ = $\displaystyle\frac{{144}}{{18}}$ = 8 metre
3. Find the length of the longest pole that can be placed in a room 12 metre long, 8 metre broad and 9 metre high.
Diagonal of room = $\sqrt {{\rm{Length}}^{\rm{2}} {\rm{ + Breadth}}^{\rm{2}} {\rm{ + Height}}^{\rm{2}} } $ = $\sqrt {12^2 + 8^2 + 9^2 } = \sqrt {289} $ = 17 metre.
Therefore, Length of longest pole = 17 metre
4. The length, breadth and height of a room are 5 metre, 4 metre and 4 metre respectively. If all the four walls of the room are to be covered with 50 cm wide wall paper, find the length of the paper required.
Area of four walls = 2 x Height (Length + Breadth) = 2 x 4 x (5 + 4) = 72 ${\rm{m}}^{\rm{2}} $
Width of the wall paper = 50 cm = 0.5 metre
Therefore, Length of the paper required = 72 $ \div $ 0.5 = 72 $ \div $ $\displaystyle\frac{1}{2}$ = 72 x 2 = 144 metre
5. How many spheres of radius 2 cm can be made by melting two spheres of radius 12 cm each?
Radius of big sphere = 12 cm
Radius of smaller sphere = 2 cm
Ratio between radii of two spheres = 12 : 2 = 6 : 1
Ratio between volumes of two spheres = $6^3 :1^3 $ = 216 : 1
Therefore, 216 speres can be made from one big sphere.
Therefore, From two big spheres, smaller spheres made = 216 x 2 = 432
6. A cube of 9 cm a side is melted and 27 small cubes are made from that. Find side of the smaller cubes.
We know, Volume of cube = ${\rm{Side}}^{\rm{3}} $
Therefore, Volume of the small cube = $\displaystyle\frac{{9^3 }}{{27}}$ = 27
Therefore, Side of the small cube = $\sqrt[3]{{27}}$ = 3 cm.
7. A box is made of 1 cm thick wood. If outer dimensions of wood are 12 cm by 10 cm by 7 cm, find volume of wood.
Outer dimensions of box = 12 cm, 10 cm, 7 cm
Inner dimensions of box = 10 cm, 8cm, 5 cm
Therefore, Volume of wood = (12 x 10 x 7) ${\rm{cm}}^{\rm{3}} $ - (10 x 8 x 5)${\rm{cm}}^{\rm{3}} $
= 840 ${\rm{cm}}^{\rm{3}} $ - 400 ${\rm{cm}}^{\rm{3}} $ = 440 ${\rm{cm}}^{\rm{3}} $.
8. How much metal is required to make a 20 metre long pipe, if its inner and outer diameter are 6 metre and 8 metre respectively.
Outer and inner radius of the pipe are 4 metre and 3 metre respectively.
Therefore, Quantity of metal required
= Outer volume of the pipe - Inner volume of the pipe
= ${\rm{\pi }}\left( {{\rm{R}}^{\rm{2}} {\rm{ - r}}^{\rm{2}} } \right){\rm{h}}$
= $\displaystyle\frac{{22}}{7} \times \left( {4^2 - 3^2 } \right)$ x 20
= $\displaystyle\frac{{22}}{7}$ x 7 x 1 x 20 = 440 ${\rm{m}}^{\rm{3}} $
Hint: Pipe is a form of cylinder.
9. A wire is drawn from a solid iron sphere of radius 6cm. Find the length of the wire, if its diameter is 6 cm.
An iron wire is a form of cylinder.
Therefore, Volume of cylinder = Volume of Sphere
Therefore, $\pi $ $\left( {{\rm{Radius of cylinder}}} \right)^{\rm{2}} $ (Height of cylinder) = $\displaystyle\frac{4}{3}\pi $ $\left( {{\rm{Radius of sphere}}} \right)^{\rm{3}} $
Therefore, Height of the cylinder = $\displaystyle\frac{4}{3}$ x $\displaystyle\frac{{\pi \left( {{\rm\text{Radius of sphere}}} \right)^{\rm{3}} }}{{\pi \left( {{\rm\text{Radius of cylinder}}} \right)^{\rm{2}} }}$
= $\displaystyle\frac{4}{3} \times \displaystyle\frac{{6 \times 6 \times 6}}{{3 \times 3}}$ = 32 cm
Therefore, Length of the wire is 32 cm.
10. A field is 90 metre long and 50 metre broad. A 25 metre long, 20 metre broad and 4 metre deep tank dug in the field and the earth taken out is spread evenly over the remaining field. How much the level of field will rise?
Area of field = 90 x 50 = 4500 ${\rm{m}}^{\rm{2}} $
Area of field dug out = 25 x 20 = 500 ${\rm{m}}^{\rm{2}} $
Therefore, Area of remaining field = 4500 ${\rm{m}}^{\rm{2}} $ - 500 ${\rm{m}}^{\rm{2}} $ = 4000 ${\rm{m}}^{\rm{2}} $
Volume of the earth dug out = 25 x 20 x 4 = 2000 ${\rm{m}}^{\rm{3}} $
Therefore, Field will rise by $\displaystyle\frac{{2000}}{{4000}}$ = 0.5 metre
MCQ's
1. The volume of a sphere is $\displaystyle\frac{{88}}{{21}} \times {14^3}c{m^3}$ The curved surface of its sphere is :
a. 2424 $c{m^2}$
b. 2446 $c{m^2}$
c. 2464 $c{m^2}$
d. 2484 $c{m^2}$
Correct Option: C
Volume of the sphere = $\displaystyle\frac{4}{3}\pi {r^3}$
$\displaystyle\frac{4}{3} \times \displaystyle\frac{{22}}{7} \times {r^3} = \displaystyle\frac{{88}}{{21}} \times {(14)^3} \Rightarrow r = 14$
Curved Surface area = $4\pi {r^2}$ = $4 \times \displaystyle\frac{{22}}{7} \times {14^2}$ = 2464 $c{m^2}$
2. If the radius of a sphere is doubled, then its volume is increased by :
a. 100%
b. 200%
c. 700%
d. 800%
Correct Option: D
Explanation:
Original volume = $\displaystyle\frac{4}{3}\pi {r^3}$
New volume = $\displaystyle\frac{4}{3}\pi {(2r)^3} = \displaystyle\frac{{32}}{3}\pi {r^3}$
Increase % = ${\left( {\displaystyle\frac{{32}}{3}\pi {r^3} \times \displaystyle\frac{3}{{4\pi {r^3}}}} \right)\% = 800\% }$
3. If the height of a cone is doubled, then its volume is increased by :
a. 100%
b. 200%
c. 300%
d. 400%
Correct Option: A
Explanation:
Original volume = $\displaystyle\frac{1}{3}\pi {r^2}h$
New volume $\displaystyle\frac{1}{3}\pi {r^2}(2h) = \displaystyle\frac{2}{3}\pi {r^2}h$
Increase % $\left( {\displaystyle\frac{{\displaystyle\frac{2}{3}\pi {r^2}h}}{{\displaystyle\frac{1}{3}\pi {r^2}h}} \times 100} \right)\% = 200\% $
4. The cost of painting the four walls of a room is Rs.350. The cost of painting a room three times in length, breadth and height will be :
a. Rs.1050
b. Rs.1400
c. Rs.3150
d. Rs.4200
Correct Option: C
Explanation:
Area of 4 walls of the room = $[2(l + b) \times h]{m^2}$
Area of 4 walls of new room = $[2(3l + 3b) \times 3h]{m^2}$ = $9[2(l + b) \times h]{m^2}$
Cost of painting the 4 walls of new room = Rs.$(9 \times 350) = Rs.3150$
5. The area of the base of a right circular cone is 154 $c{m^2}$ and its height is 14 cm. The curved surface of the cone is :
a. $(154 \times \sqrt 5 )c{m^2}$
b. 11 $c{m^2}$
c. $(154 \times \sqrt 7 )c{m^2}$
d. 5324 $c{m^2}$
Correct Option: A
Explanation:
$\displaystyle\frac{{22}}{7} \times {r^2} = 154 \Rightarrow {r^2} = \left( {154 \times \displaystyle\frac{7}{{22}}} \right)$ = 49 or r = 7 cm
Now, r = 7 and h = 14.
So, l = $\sqrt {{{(7)}^2} + {{(14)}^2}} $
= $\sqrt {245} = 7\sqrt 5 $ cm
Area of curved surface = $\pi rl$ = $\left( {\displaystyle\frac{{22}}{7} \times 7 \times 7\sqrt 5 } \right)c{m^2} = 154\sqrt 5 {\rm{ }}c{m^2}$
6. The material of a cone is converted into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm, the height of the cone is :
a. 10 cm
b. 15 cm
c. 18 cm
d. 24 cm
Correct Option: B
Explanation:
$\displaystyle\frac{1}{3}\pi {r^2} \times h = \pi {h^2} \times 5$ or h = 15 cm
7. A sold consists of a circular cylinder with an exact fitting right circular cone placed on the top. The height of the cone is h. If the total volume of the solid is three times the volume of the cone, then the height of the cylinder is :
a. 2 h
b. 4 h
c. $\displaystyle\frac{{2h}}{3}$
d. $\displaystyle\frac{{3h}}{3}$
Correct Option: C
Explanation:
Let the height of the cylinder be H and its radius = r.
Then, $\pi {r^2}H + \displaystyle\frac{1}{3}\pi {r^2}h$ = $ 3 \times \displaystyle\frac{1}{3}\pi {r^2}h$
$\Rightarrow \pi {r^2}H = \displaystyle\frac{2}{3}\pi {r^2}h$ or H = $\displaystyle\frac{2}{3}h$
8. If the volumes of two cones are in the ratio 1:4 and their diameters are in the ratio 4:5, then the ratio of their height is :
a. 1:5
b. 5:4
c. 5:16
d. 25:64
Correct Option: D
Explanation:
Since the diameters are in the ratio 4:5, it follows that their radii are in the ratio 4:5. Let them be 4 r and 5 r.
Let the height be h and H.
Ratio of volumes = $\displaystyle\frac{{\displaystyle\frac{1}{3}\pi \times {{(4r)}^2} \times h}}{{\displaystyle\frac{1}{3}\pi \times {{(5r)}^2} \times H}} = \displaystyle\frac{{16h}}{{25H}}$
$\displaystyle\frac{{16h}}{{25H}} = \displaystyle\frac{1}{4}{\rm{ or }}\displaystyle\frac{h}{H}{\rm{ = }}\left( {\displaystyle\frac{1}{4} \times \displaystyle\frac{{25}}{{16}}} \right){\rm{ = }}\displaystyle\frac{{25}}{{64}}{\rm{ = 25:64}}$
9. If a rightg circular cone of vertical height 24 cm has a volume of 1232 $c{m^3}$, then the area of its curved surface is :
a. 1254 $c{m^2}$
b. 704 $c{m^2}$
c. 550 $c{m^2}$
d. 154 $c{m^2}$
Correct Option: C
Explanation :
$\displaystyle\frac{1}{3} \times \displaystyle\frac{{22}}{7} \times {r^2} \times 24 = 1232$ or
$\left( {1232 \times \displaystyle\frac{7}{{22}} \times \displaystyle\frac{3}{{24}}} \right) = 49$
$\Rightarrow {r^2} = \left( {1232 \times \displaystyle\frac{7}{{22}} \times \displaystyle\frac{3}{{24}}} \right) = 49$
$\Rightarrow $ r = 7 cm
Now r = 7 and h = 24, So, l = $\sqrt {{7^2} + {{(24)}^2}} = \sqrt {625} = 25$ cm
Curved surface area = $\pi {\rm{rl}}$ = $\left( {\displaystyle\frac{{22}}{7} \times 7 \times 25} \right)c{m^2} = 550c{m^2}$
10. A cylindrical piece of metal of radius 2cm and height 6 cm is shaped into a cone of same radius. The height of the cone is :
a. 18cm
b. 14cm
c. 12cm
d. 8 cm
Correct Option: A
Explanation:
${\displaystyle\frac{1}{3}\pi \times {{(2)}^2} \times h = \pi \times {{(2)}^2} \times 6 \Rightarrow h = 18}$ cm
11. The radii of two cylinder are in the ratio of 2:3 and their heights are in the ratio 5:3. The ratio of their volumes is :
a. 27:20
b. 20:27
c. 4 : 9
d. 9 : 4
Correct Option: B
Explanation:
Let their radii be 2 r and 3r and heights 5h and 3h respectively. Ratio of their volumes.
=$\displaystyle\frac{{\pi {{(2r)}^2} \times 5h}}{{\pi {{(3r)}^2} \times 3h}} = \displaystyle\frac{{20}}{{27}} = 20:27$
12. If the volume and surface area of a sphere are numerically the same, then its radius is :
a. 1 unit
b. 2 units
c. 3 units
d. 4 units
Correct Option: C
Explanation:
$\displaystyle\frac{4}{3}\pi {r^3} = 4\pi {r^2} \Rightarrow r = 3$ units
13. A spherical lead ball of radius 10 cm is melted and small lead balls of radius 5 mm are made. The total number of possible small lead balls is :
a. 800
b. 125
c. 400
d. 8000
Correct Option: D
Explanatioin:
Number of balls = $\displaystyle\frac{{{\rm\text{Volume of big ball}}}}{{{\rm\text{Volume of small ball}}}}$ $ = \displaystyle\frac{{\displaystyle\frac{4}{3} \times \pi \times 10 \times 10 \times 10}}{{\displaystyle\frac{4}{3} \times \pi \times 0.5 \times 0.5 \times 0.5}} = 800$
14. The radii of two spheres are in the ratio 1:2. The ratio of their surface areas is :
a. 1 : 2
b. 1 : 4
c. 1 : $\sqrt 2 $
d. 3 : 8
Correct Option: B
Explanation:
Let their radii be x and 2 x.
Ratio of their surface areas = $\displaystyle\frac{{4\pi {x^2}}}{{4\pi {{(2x)}^2}}} = \displaystyle\frac{1}{4} = 1:4$
15. A right cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is :
a. 3 : 5
b. 2 : 5
c. 3 : 1
d. 1 : 3
Correct Option: D
Explanation :
Let the height of cylinder = h
and height of cone = H
Then, ${\pi ^2}h = \displaystyle\frac{1}{3}\pi {r^2}H$ or $\displaystyle\frac{h}{H} = \displaystyle\frac{1}{3} = 1:3$
16. The radius of a circular cylinder is the same as that of a sphere. Their volumes are equal. The height of the cylinder is :
a. $\displaystyle\frac{4}{3}$ times its radius
b. $\displaystyle\frac{2}{3}$ times its radius
c. equal to radius
d. equal to its diameter
Correct Option: A
Explanation:
$\displaystyle\frac{4}{3}\pi {r^3} = \pi {r^2}h \Rightarrow h = \displaystyle\frac{4}{3}r$
Height = $\displaystyle\frac{4}{3}$ times of its radius.
17. The number of solid spheres, each of diameter 6 cm, that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is :
a. 3
b. 4
c. 5
d. 6
Correct Option: C
Explanation:
Let the number of spheres be x.
Then, $x \times \displaystyle\frac{4}{3}\pi \times {(3)^3} = \pi \times {(2)^2} \times 45$
or 36x = 180 or x = $\displaystyle\frac{{180}}{{36}} = 5$
18. The length of the wire of 0.2 mm radius that can be drawn after melting a solid copper sphere of diameter 18 cm is :
a. 24.3 m
b. 243 m
c. 2430 m
d. 24300m
Correct Option: D
Explanation:
Radius of sphere = 9 cm
Volume of sphere = $\left[ {\displaystyle\frac{4}{3} \times \pi {{(9)}^3}} \right]c{m^3} = (972\pi )c{m^3}$ = $\displaystyle\frac{1}{{50}}$ cm
Let the length be = x cm
Then, $972\pi = \pi \times {\left( {\displaystyle\frac{1}{{50}}} \right)^2} \times x$ $ \Rightarrow x = (972 \times 50 \times 50)$ cm
Length of wire = $\left( {\displaystyle\frac{{972 \times 50 \times 50}}{{100}}} \right)$ m = 24300 m
19. The radius of a wire is decreased to one-third. If volume remains the same, length will increase:
a. 1 time
b. 3 times
c. 6 times
d. 9 times
Correct Option: D
Explanation:
Let original radius = r and original length = h
Now radius = $\displaystyle\frac{1}{3}r$, Let new length = H
Then, $\pi {r^2}{\rm{ h = }}\pi {\left( {\displaystyle\frac{1}{3}r} \right)^2} \times H = \displaystyle\frac{{\pi {r^2}H}}{9}$ H = 9h
Thus, the length becomes 9 times.
20. If the volumes of two cubes are in the ratio 8:1, the ratio of their edges is :
a. 8 : 1
b. 2$\sqrt 2 $ : 1
c. 2 : 1
d. None of these
Correct Option: C
Explanation:
Let their volumes be $8{x^2}$ and ${x^3}$ respectively
Then, their edges are
2x and x respectively
Ratio of their edges = 2 : 1
21. A metal sheet 27 cm long 8 cm broad and 1 cm thick is melted into a cube. The difference between the surface areas of two solids is :
a. 284 $c{m^2}$
b. 286 $c{m^2}$
c. 296 $c{m^2}$
d. 300 $c{m^2}$
Correct Option: B
Explanatioin:
Surface area of the metal sheet = 2(lb + bh + lh) = $2\times(27\times8+8\times1+27\times1)$=502
Volume of sheet = $(27 \times 8 \times 1){\rm{ }}c{m^2} = 216{\rm{ }}c{m^2}$
Volume of cube formed = 216 $c{m^2}$
Edge of the cube = ${(6 \times 6 \times 6)^{1/3}} = 6$ cm
Surface area of the cube formed = $\left[ {6 \times {{(6)}^2}} \right]$ $c{m^2}$ = 216 $c{m^2}$
Difference in areas = (502-216)$c{m^2}$=286 $c{m^2}$
22. A wooden box of dimensions $8m \times 7m \times 6m$ is to carrry rectangular boxes of dimensions $8cm \times 7cm \times 6cm$ . The maximum number of boxes that can be carried in 1 wooden box is :
a. 1200000
b. 1000000
c. 9800000
d. 7500000
Correct Option: B
Explanation:
Number of boxes = $\displaystyle\frac{{{\rm\text{Volume of wooden box in c}}{{\rm{m}}^{\rm{3}}}}}{{{\rm\text{Volume of 1 small ball}}}}$ = $\displaystyle\frac{{800 \times 700 \times 600}}{{8 \times 7 \times 6}} = 1000000$
23. If the length, breadth and the height of a cuboid are in the ratio 6:5:4 and if the total surface area is 33300 $c{m^2}$, then the length , breadth and height in cms, are respectively.
a. 90,85,60
b. 85,75,60
c. 90,75,70
d. 90,75,60
Correct Option: D
Explanation:
Let length = 6x, breadth = 5x and height =4x in cm
$2(6x \times 5x + 5x \times 4x + 6x \times 4x) = 33300$
$148{x^2} = 33300 \Rightarrow {x^2}$=$\displaystyle\frac{{33300}}{{148}} = 225 \Rightarrow x = 15$
Length = 90 cm, Breadth = 75 cm and Height = 60 cm
24. The maximum length of a pencil that can be kept in a rectangular box of dimensions $8cm \times 6cm \times 2cm$, is :
a. $2\sqrt {13} $ cm
b. $2\sqrt {14} $ cm
c. $2\sqrt {26} $ cm
d. $10\sqrt 2 $ cm
Correct Option: C
Explanation:
Length of pencil = $\sqrt {{{(8)}^2} + {{(6)}^2} + {{(2)}^2}} $ cm = $\sqrt {104} $ cm = 2$\sqrt {26} $ cm
25. The surface area of a cube is 726 ${m^2}$.Its volume is:
a. 1300 ${m^3}$
b. 1331 ${m^3}$
c. 1452 ${m^3}$
d. 1542 ${m^3}$
Correct Option: B
Explanation:
$6{a^2} = 726 \Rightarrow {a^2} = 121 \Rightarrow a = 11$ cm
Volume of the cube = $(11 \times 11 \times 11)c{m^3}$ = 1331$c{m^3}$
MCQ's
1. The volume of a sphere is $\displaystyle\frac{{88}}{{21}} \times {14^3}c{m^3}$ The curved surface of its sphere is :
a. 2424 $c{m^2}$
b. 2446 $c{m^2}$
c. 2464 $c{m^2}$
d. 2484 $c{m^2}$
Correct Option: C
Volume of the sphere = $\displaystyle\frac{4}{3}\pi {r^3}$
$\displaystyle\frac{4}{3} \times \displaystyle\frac{{22}}{7} \times {r^3} = \displaystyle\frac{{88}}{{21}} \times {(14)^3} \Rightarrow r = 14$
Curved Surface area = $4\pi {r^2}$ = $4 \times \displaystyle\frac{{22}}{7} \times {14^2}$ = 2464 $c{m^2}$
2. If the radius of a sphere is doubled, then its volume is increased by :
a. 100%
b. 200%
c. 700%
d. 800%
Correct Option: D
Explanation:
Original volume = $\displaystyle\frac{4}{3}\pi {r^3}$
New volume = $\displaystyle\frac{4}{3}\pi {(2r)^3} = \displaystyle\frac{{32}}{3}\pi {r^3}$
Increase % = ${\left( {\displaystyle\frac{{32}}{3}\pi {r^3} \times \displaystyle\frac{3}{{4\pi {r^3}}}} \right)\% = 800\% }$
3. If the height of a cone is doubled, then its volume is increased by :
a. 100%
b. 200%
c. 300%
d. 400%
Correct Option: A
Explanation:
Original volume = $\displaystyle\frac{1}{3}\pi {r^2}h$
New volume $\displaystyle\frac{1}{3}\pi {r^2}(2h) = \displaystyle\frac{2}{3}\pi {r^2}h$
Increase % $\left( {\displaystyle\frac{{\displaystyle\frac{2}{3}\pi {r^2}h}}{{\displaystyle\frac{1}{3}\pi {r^2}h}} \times 100} \right)\% = 200\% $
4. The cost of painting the four walls of a room is Rs.350. The cost of painting a room three times in length, breadth and height will be :
a. Rs.1050
b. Rs.1400
c. Rs.3150
d. Rs.4200
Correct Option: C
Explanation:
Area of 4 walls of the room = $[2(l + b) \times h]{m^2}$
Area of 4 walls of new room = $[2(3l + 3b) \times 3h]{m^2}$ = $9[2(l + b) \times h]{m^2}$
Cost of painting the 4 walls of new room = Rs.$(9 \times 350) = Rs.3150$
5. The area of the base of a right circular cone is 154 $c{m^2}$ and its height is 14 cm. The curved surface of the cone is :
a. $(154 \times \sqrt 5 )c{m^2}$
b. 11 $c{m^2}$
c. $(154 \times \sqrt 7 )c{m^2}$
d. 5324 $c{m^2}$
Correct Option: A
Explanation:
$\displaystyle\frac{{22}}{7} \times {r^2} = 154 \Rightarrow {r^2} = \left( {154 \times \displaystyle\frac{7}{{22}}} \right)$ = 49 or r = 7 cm
Now, r = 7 and h = 14.
So, l = $\sqrt {{{(7)}^2} + {{(14)}^2}} $
= $\sqrt {245} = 7\sqrt 5 $ cm
Area of curved surface = $\pi rl$ = $\left( {\displaystyle\frac{{22}}{7} \times 7 \times 7\sqrt 5 } \right)c{m^2} = 154\sqrt 5 {\rm{ }}c{m^2}$
6. The material of a cone is converted into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm, the height of the cone is :
a. 10 cm
b. 15 cm
c. 18 cm
d. 24 cm
Correct Option: B
Explanation:
$\displaystyle\frac{1}{3}\pi {r^2} \times h = \pi {h^2} \times 5$ or h = 15 cm
7. A sold consists of a circular cylinder with an exact fitting right circular cone placed on the top. The height of the cone is h. If the total volume of the solid is three times the volume of the cone, then the height of the cylinder is :
a. 2 h
b. 4 h
c. $\displaystyle\frac{{2h}}{3}$
d. $\displaystyle\frac{{3h}}{3}$
Correct Option: C
Explanation:
Let the height of the cylinder be H and its radius = r.
Then, $\pi {r^2}H + \displaystyle\frac{1}{3}\pi {r^2}h$ = $ 3 \times \displaystyle\frac{1}{3}\pi {r^2}h$
$\Rightarrow \pi {r^2}H = \displaystyle\frac{2}{3}\pi {r^2}h$ or H = $\displaystyle\frac{2}{3}h$
8. If the volumes of two cones are in the ratio 1:4 and their diameters are in the ratio 4:5, then the ratio of their height is :
a. 1:5
b. 5:4
c. 5:16
d. 25:64
Correct Option: D
Explanation:
Since the diameters are in the ratio 4:5, it follows that their radii are in the ratio 4:5. Let them be 4 r and 5 r.
Let the height be h and H.
Ratio of volumes = $\displaystyle\frac{{\displaystyle\frac{1}{3}\pi \times {{(4r)}^2} \times h}}{{\displaystyle\frac{1}{3}\pi \times {{(5r)}^2} \times H}} = \displaystyle\frac{{16h}}{{25H}}$
$\displaystyle\frac{{16h}}{{25H}} = \displaystyle\frac{1}{4}{\rm{ or }}\displaystyle\frac{h}{H}{\rm{ = }}\left( {\displaystyle\frac{1}{4} \times \displaystyle\frac{{25}}{{16}}} \right){\rm{ = }}\displaystyle\frac{{25}}{{64}}{\rm{ = 25:64}}$
9. If a rightg circular cone of vertical height 24 cm has a volume of 1232 $c{m^3}$, then the area of its curved surface is :
a. 1254 $c{m^2}$
b. 704 $c{m^2}$
c. 550 $c{m^2}$
d. 154 $c{m^2}$
Correct Option: C
Explanation :
$\displaystyle\frac{1}{3} \times \displaystyle\frac{{22}}{7} \times {r^2} \times 24 = 1232$ or
$\left( {1232 \times \displaystyle\frac{7}{{22}} \times \displaystyle\frac{3}{{24}}} \right) = 49$
$\Rightarrow {r^2} = \left( {1232 \times \displaystyle\frac{7}{{22}} \times \displaystyle\frac{3}{{24}}} \right) = 49$
$\Rightarrow $ r = 7 cm
Now r = 7 and h = 24, So, l = $\sqrt {{7^2} + {{(24)}^2}} = \sqrt {625} = 25$ cm
Curved surface area = $\pi {\rm{rl}}$ = $\left( {\displaystyle\frac{{22}}{7} \times 7 \times 25} \right)c{m^2} = 550c{m^2}$
10. A cylindrical piece of metal of radius 2cm and height 6 cm is shaped into a cone of same radius. The height of the cone is :
a. 18cm
b. 14cm
c. 12cm
d. 8 cm
Correct Option: A
Explanation:
${\displaystyle\frac{1}{3}\pi \times {{(2)}^2} \times h = \pi \times {{(2)}^2} \times 6 \Rightarrow h = 18}$ cm
11. The radii of two cylinder are in the ratio of 2:3 and their heights are in the ratio 5:3. The ratio of their volumes is :
a. 27:20
b. 20:27
c. 4 : 9
d. 9 : 4
Correct Option: B
Explanation:
Let their radii be 2 r and 3r and heights 5h and 3h respectively. Ratio of their volumes.
=$\displaystyle\frac{{\pi {{(2r)}^2} \times 5h}}{{\pi {{(3r)}^2} \times 3h}} = \displaystyle\frac{{20}}{{27}} = 20:27$
12. If the volume and surface area of a sphere are numerically the same, then its radius is :
a. 1 unit
b. 2 units
c. 3 units
d. 4 units
Correct Option: C
Explanation:
$\displaystyle\frac{4}{3}\pi {r^3} = 4\pi {r^2} \Rightarrow r = 3$ units
13. A spherical lead ball of radius 10 cm is melted and small lead balls of radius 5 mm are made. The total number of possible small lead balls is :
a. 800
b. 125
c. 400
d. 8000
Correct Option: D
Explanatioin:
Number of balls = $\displaystyle\frac{{{\rm\text{Volume of big ball}}}}{{{\rm\text{Volume of small ball}}}}$ $ = \displaystyle\frac{{\displaystyle\frac{4}{3} \times \pi \times 10 \times 10 \times 10}}{{\displaystyle\frac{4}{3} \times \pi \times 0.5 \times 0.5 \times 0.5}} = 800$
14. The radii of two spheres are in the ratio 1:2. The ratio of their surface areas is :
a. 1 : 2
b. 1 : 4
c. 1 : $\sqrt 2 $
d. 3 : 8
Correct Option: B
Explanation:
Let their radii be x and 2 x.
Ratio of their surface areas = $\displaystyle\frac{{4\pi {x^2}}}{{4\pi {{(2x)}^2}}} = \displaystyle\frac{1}{4} = 1:4$
15. A right cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is :
a. 3 : 5
b. 2 : 5
c. 3 : 1
d. 1 : 3
Correct Option: D
Explanation :
Let the height of cylinder = h
and height of cone = H
Then, ${\pi ^2}h = \displaystyle\frac{1}{3}\pi {r^2}H$ or $\displaystyle\frac{h}{H} = \displaystyle\frac{1}{3} = 1:3$
16. The radius of a circular cylinder is the same as that of a sphere. Their volumes are equal. The height of the cylinder is :
a. $\displaystyle\frac{4}{3}$ times its radius
b. $\displaystyle\frac{2}{3}$ times its radius
c. equal to radius
d. equal to its diameter
Correct Option: A
Explanation:
$\displaystyle\frac{4}{3}\pi {r^3} = \pi {r^2}h \Rightarrow h = \displaystyle\frac{4}{3}r$
Height = $\displaystyle\frac{4}{3}$ times of its radius.
17. The number of solid spheres, each of diameter 6 cm, that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is :
a. 3
b. 4
c. 5
d. 6
Correct Option: C
Explanation:
Let the number of spheres be x.
Then, $x \times \displaystyle\frac{4}{3}\pi \times {(3)^3} = \pi \times {(2)^2} \times 45$
or 36x = 180 or x = $\displaystyle\frac{{180}}{{36}} = 5$
18. The length of the wire of 0.2 mm radius that can be drawn after melting a solid copper sphere of diameter 18 cm is :
a. 24.3 m
b. 243 m
c. 2430 m
d. 24300m
Correct Option: D
Explanation:
Radius of sphere = 9 cm
Volume of sphere = $\left[ {\displaystyle\frac{4}{3} \times \pi {{(9)}^3}} \right]c{m^3} = (972\pi )c{m^3}$ = $\displaystyle\frac{1}{{50}}$ cm
Let the length be = x cm
Then, $972\pi = \pi \times {\left( {\displaystyle\frac{1}{{50}}} \right)^2} \times x$ $ \Rightarrow x = (972 \times 50 \times 50)$ cm
Length of wire = $\left( {\displaystyle\frac{{972 \times 50 \times 50}}{{100}}} \right)$ m = 24300 m
19. The radius of a wire is decreased to one-third. If volume remains the same, length will increase:
a. 1 time
b. 3 times
c. 6 times
d. 9 times
Correct Option: D
Explanation:
Let original radius = r and original length = h
Now radius = $\displaystyle\frac{1}{3}r$, Let new length = H
Then, $\pi {r^2}{\rm{ h = }}\pi {\left( {\displaystyle\frac{1}{3}r} \right)^2} \times H = \displaystyle\frac{{\pi {r^2}H}}{9}$ H = 9h
Thus, the length becomes 9 times.
20. If the volumes of two cubes are in the ratio 8:1, the ratio of their edges is :
a. 8 : 1
b. 2$\sqrt 2 $ : 1
c. 2 : 1
d. None of these
Correct Option: C
Explanation:
Let their volumes be $8{x^2}$ and ${x^3}$ respectively
Then, their edges are
2x and x respectively
Ratio of their edges = 2 : 1
21. A metal sheet 27 cm long 8 cm broad and 1 cm thick is melted into a cube. The difference between the surface areas of two solids is :
a. 284 $c{m^2}$
b. 286 $c{m^2}$
c. 296 $c{m^2}$
d. 300 $c{m^2}$
Correct Option: B
Explanatioin:
Surface area of the metal sheet = 2(lb + bh + lh) = $2\times(27\times8+8\times1+27\times1)$=502
Volume of sheet = $(27 \times 8 \times 1){\rm{ }}c{m^2} = 216{\rm{ }}c{m^2}$
Volume of cube formed = 216 $c{m^2}$
Edge of the cube = ${(6 \times 6 \times 6)^{1/3}} = 6$ cm
Surface area of the cube formed = $\left[ {6 \times {{(6)}^2}} \right]$ $c{m^2}$ = 216 $c{m^2}$
Difference in areas = (502-216)$c{m^2}$=286 $c{m^2}$
22. A wooden box of dimensions $8m \times 7m \times 6m$ is to carrry rectangular boxes of dimensions $8cm \times 7cm \times 6cm$ . The maximum number of boxes that can be carried in 1 wooden box is :
a. 1200000
b. 1000000
c. 9800000
d. 7500000
Correct Option: B
Explanation:
Number of boxes = $\displaystyle\frac{{{\rm\text{Volume of wooden box in c}}{{\rm{m}}^{\rm{3}}}}}{{{\rm\text{Volume of 1 small ball}}}}$ = $\displaystyle\frac{{800 \times 700 \times 600}}{{8 \times 7 \times 6}} = 1000000$
23. If the length, breadth and the height of a cuboid are in the ratio 6:5:4 and if the total surface area is 33300 $c{m^2}$, then the length , breadth and height in cms, are respectively.
a. 90,85,60
b. 85,75,60
c. 90,75,70
d. 90,75,60
Correct Option: D
Explanation:
Let length = 6x, breadth = 5x and height =4x in cm
$2(6x \times 5x + 5x \times 4x + 6x \times 4x) = 33300$
$148{x^2} = 33300 \Rightarrow {x^2}$=$\displaystyle\frac{{33300}}{{148}} = 225 \Rightarrow x = 15$
Length = 90 cm, Breadth = 75 cm and Height = 60 cm
24. The maximum length of a pencil that can be kept in a rectangular box of dimensions $8cm \times 6cm \times 2cm$, is :
a. $2\sqrt {13} $ cm
b. $2\sqrt {14} $ cm
c. $2\sqrt {26} $ cm
d. $10\sqrt 2 $ cm
Correct Option: C
Explanation:
Length of pencil = $\sqrt {{{(8)}^2} + {{(6)}^2} + {{(2)}^2}} $ cm = $\sqrt {104} $ cm = 2$\sqrt {26} $ cm
25. The surface area of a cube is 726 ${m^2}$.Its volume is:
a. 1300 ${m^3}$
b. 1331 ${m^3}$
c. 1452 ${m^3}$
d. 1542 ${m^3}$
Correct Option: B
Explanation:
$6{a^2} = 726 \Rightarrow {a^2} = 121 \Rightarrow a = 11$ cm
Volume of the cube = $(11 \times 11 \times 11)c{m^3}$ = 1331$c{m^3}$