1. Overfishing is a serious environmental issue. It has been determined by the scientists that if the net of a trawler has mesh size x cm (a square mesh), then the percentage of fish entering the net that are caught in the net is (100 - 0.04x^2- 0.24x). For example, if the mesh size is zero, 100% of the fish that enter the net will be caught.A trawler with net with a square mesh, that was suspect of using an illegal size net, dropped its net to the ocean floor near the Andamans and the coast guard, officials arrested the crew. The scientists later looked the size of the fish caught, and estimated that for the net used by the trawler, atleast 97.8% of the fish entering the net would be caught. What is the maximum value of x for the net used by the trawler?
a. 5 | b. 4.5 |
c. 7 | d. None of the above answer |
Explanation:
For some x, 97.8% fish was caught. So
⇒ 100 - 0.04x2- 0.24x = 97.8
⇒ 0.04x2 + 0.24x = 2.2
⇒ 4x2+ 24x = 220
⇒ x2+ 6x - 55 = 0
Solving we get x = 5 and -11
So x = 5 is correct option.
2. Oranges can be packed in sets of 10 oranges in box type A or 25 oranges in box type B. A carton comprising of 1000 oranges of type a and b is packed. How many different combinations are possible in the number of type A and type B boxes while organizing the oranges?
a. 21 | b. 20 |
c. 19 | d. 18 |
Explanation:
Given that 10a + 25b = 1000 ⇒ 2a + 5b = 200
One general solution for the above equation is when a = 0, then b = 40.
To get other solutions, $a$ is increased by 5 and $b$ is decreased by 2. So next solution is (5, 38)
Now $b$ is reduced upto 0.
So total solutions = $\dfrac{{40 - 0}}{2} + 1$ = 21
(☕ Solving equations in integers is an interesting branch of mathematics. These equations are called diophantine equations. Click here to read the article on this topic)
3. In a potato race, 20 potatoes are placed in a line of intervals of 4 meters with the first potato 24 meters from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
a. 2400 | b. 1440 |
c. 2480 | d. 1240 |
Explanation:
Given, total number of potatos = 20.
First potato 24 metres from the starting point. There are 4 meters in the intervals. A contestant is required to bring the potatoes back to the starting place one at a time. So for the first potato he has to travel 48 meters, for second 56 meters ...
48,56,64...........20 terms.
a = 48, d= 8, n = 20.
Sum of n terms in A.P = ${S_n} = \dfrac{n}{2}\left[ {2a + (n - 1)d} \right]$
${S_{20}} = \dfrac{{20}}{2}\left[ {2 \times 48 + (20 - 1)8} \right]$
${S_{20}} = \dfrac{{20}}{2}\left[ {96 + 152} \right]$
${S_{20}} = 10 \times 248 = 2480$
∴ 2480 meters he run in bringing back all the potatoes.
4. In this question A^B means A raised to the power of B Start with the integers from 1 to 10^2012. Replace each of them by the sum of its digits to get a string of 10^2012 numbers. Keep doing this until you get 10^2012 single digit numbers. Let m be the number of 1's and n be the number of 2's. Then m - n
a. 1 | b. 3 |
c. 2 | d. 0 |
Explanation:
We divide all the numbers into groups of 9. (1 to 9), (10 to 18).....
Now when we divide each term in the first group by 9, we get 1, 2, 3 ..0 as remainders. Now digit sum is nothing but finding remainder when a number is divided by 9. So the last term, 10^2012 gives remainder 1 when divided by 9. So there is one "1" extra than 2's.
5. On a certain assembly line, the rejection rate for Hyundai i10s production was 4 percent, for Hyundai i20s production 8 percent and for the 2 cars combined 7 percent. What was the ratio of Hyundais i10 production?
a. 3/1 | b. 2/1 |
c. 1/1 | d. 1/2 |
Explanation:
Simple weighted average rule can be applied. Let $a$ cars of i10's and $b$ cars of i20s are made.
$\dfrac{{4(a) + 8(b)}}{{a + b}} = 7$
$4(a) + 8(b) = 7a + 7b$
3a = b ⇒ a/b = 3/1
6. Two decks of cards are there. Each deck contains 20 cards, with numbers from 1 to 20 written on them. A card is drawn of random from each deck, getting the numbers x and y What is the probability that log x + log y is a positive integer. Logs are taken to the base 10.
a. 3/200 | b. 29/200 |
c. 7/400 | d. 1/50 |
Explanation:
Log x + log y = log(xy)
log xy is integer when (x,y) = (1, 10), (10, 1), (10, 10), (5, 20), (20, 5), (2, 5), (5, 2)
So required probability = 7/400
7. Let a, b, c, d and e be distinct integers in ascending order such that(76-a)(76-b)(76-c)(76-d)(76-e) = 1127. What is a + b + c + d
a. 30 | b. 274 |
c. 334 | d. 136 |
Explanation:
(Personally I liked the beauty of this question)
Product of 5 terms equal to 1127. As all the five terms are integers, given product should be a product of 5 numbers. Now factorize 1127.
1127 = 72 × 23 = 7 × 7 × 23
But given that all the a, b, c, d, e are distinct. And we are getting only 3 terms with 7 repeats.
Now the logic is, integers means positive and negative, 7 and - 7 possible and 1, - 1 also possible . As a,b, c, d, e are in ascending order, the factors should be in decreasing order. So (23, 7, 1, -1, -7)
Now a = 53; b = 69; c = 75; d = 77
a + b + c + d = 274.
8. In how many ways a team of 11 must be selected a team 5 men and 11 women such that the team must comprise of not more than 3 men.
a. 1565 | b. 2256 |
c. 2456 | d. 1243 |
Explanation:
Maximum 3 men can be played which means there can be 0, 1, 2, 3 men in the team.
${(^5}{C_0}{ \times ^{11}}{C_{11}}) + {(^5}{C_1}{ \times ^{11}}{C_{10}})$ + ${(^5}{C_2}{ \times ^{11}}{C_9}) + {(^5}{C_3}{ \times ^{11}}{C_8})$ = 2256
9. In this question, A^B refers to A raised to the power B.Ten tickets numbered 1, 2, 3, ..., 10. Six tickets are selected at random one of a time with replacement. The probability of the largest number appearing on the selected ticket is 7 is
a. (7^6 +1)/10^6 | b. (7^6 - 6^6)/10^6 |
c. (7^6+6^6)/10^6 | d. 6^6/10^6 |
Explanation:
Number of ways of selecting six numbers out of 10 = 106
Now number of ways of selecting 6 numbers from 1 to 7 = 76
Number of ways of selecting 6 numbers from 1 to 6 = 66
So number of ways of selecting 7 numbers of which 7 is maximum = 76 - 66
Required probability = (76 - 66 ) / 106
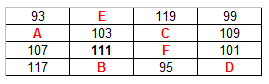
10. In the above table, the sum of numbers in each column, each row and the two diagonals are the same. What is the value of (A*B)+(c*d) - (E*F)?
Explanation:
We have to form equations.
311 + E - - - - -(1)
212 + A + C - - - - -(2)
319+ F = x - - - - -(3)
212 + B + D = x - - - - -(4)
317 + A = x - - - - -(5)
214 + E + B = x - - - - -(6)
214 + C + F = x - - - - -(7)
309 + D = x - - - - -(8)
196 + F + D = x - - - - -(9)
327 + C = x - - - - -(10)
Here 7 variables but 10 equations. So can be solved easily.
From (2) and (10)
212 + A + C = 327 + C ⇒ A = 115
From (5), x = 317 + 115 = 432
From (1), E = 432 - 311 = 121
From (3), F = 432 - 319 = 113
From (8), D = 432 - 309 = 123
From (4), B = 432 - 123 - 212 = 97
From (10), C = 432 - 327 = 105
So (A*B)+(c*d) - (E*F) = (115*97) + (105*123) - (121*113) = 10397
11. In the medieval times, the sheikdom of Al kurazi had a proud tradition of inventing their own measurements units. The unit for distance was du, and the unit of time was pu. Unfortunately exactly what these measurement units are in modern terminology has been lost. The sheikh of Al Kurazi had built a huge mansion in the desert (near an oasis) with a circular wall around it, and the wall had four gates pointing north, south, east and west. He had built three observation towers, one 144 du to the north of the north gate, one 135 du to the east of the south gate, and one 7 1/2 du to the east of the east gate. They had been aligned to be all in a straight line passing thru the oasis. What was the diameter of the wall that surrounded the city (in Du)?
a. 178b. 183
c. 180
d. 181
Answer: c
Explanation:
$\triangle AOC, \triangle AST $ are similar triangles. So
$\Rightarrow\dfrac{AO}{OC}=\dfrac{AS}{ST}$
$\Rightarrow\dfrac{144+r}{r+7.5}=\dfrac{144+2r}{135}$
Solving we get r = 90. So diameter of the wall = 180 du
12. What is the minimum value of abs(187m – 396n – 526) as m, n take all integer values? Here abs is the absolute value function (that is, if x > 0, then abs(x) = x and if x < 0, then abs(x) = – x).
a. 0
b. 9
c. 2
d. 1
Answer: c
Explanation:
We have to find the minimum value of $|(187m - 396n - 526)|$ = $|(187m - 396n) - 526)|$
If $|(187m - 396n)|$ is 526 then the given expression attains minimum.
Now observe carefully, both 187, 386 are multiples of 11. So $|11(17m - 36n)|$ may not equal to exactly 526 but some value near to 526. Nearest multiple of 11 is 528.
Now $|11(17m - 36n)|=528$
$\Rightarrow(17m - 36n)=48$
$\Rightarrow m=\dfrac{48+36n}{17}$
$\Rightarrow m=2 + 2n+\dfrac{14+2n}{17}$
So for n = 10, we get m = 24.
So $|11(17m - 36n)|$ = 528 So minimum value of the given expression is 2.
3. In this problem, ABS(x) provides absolute value of x, without regard to its sign. For example ABS(3) = ABS(-3) = 3
The graphs of y = – ABS(x – a) + b and y = – ABS(x – c) + d intersect at points (2,5) and (8, 3).
Find a + c
a. 8
b. 10
c. 7
d. 5
Answer: a
Explanation:
Both curves intersect at (2, 5)
So 5 = – |2 – a| + b $\Rightarrow$ 5 + |2 – a| – b = 0 - - - (1)
5 = – |2 – c| + d $\Rightarrow$ 5 + |2 – c| – d = 0 - - - (2)
Also,
3 = – |8 – a| + b $\Rightarrow$ 3 + |8 – a| – b = 0 - - - (3)
3 = – |8 – c| + d $\Rightarrow$ 3 + |8 – c| – d = 0- - - (4)
Equating 1 and 3, 5 + |2 – a| = 3 + |8 – a| $\Rightarrow$ 2 + |2 – a| = |8– a|
So a = 4
Similarly if we equate 2 and 4, we get c = 4
a + c = 8
14. Professor nitwit obtains a hash number of a given positive integer > 3 as follows. He substracts 2 from the number (to get the new number), and multiplies the new number by 2 to get a term. He repeats this with the new number (to get newer numbers and terms) until the number becomes 2 or 1. The hash is defined as the sum of all the numbers generated in the process.
For example, with the number 5, he multiples (5-2 = 3) by 2 to get the first term 6. He multiplies (3 - 2 = 1) by 2 to get the second term 2. As the number has become 1, he stops. The hash is the sum of the two numbers (6+2) = 8.
If Professor Nitwit is given 3 numbers 19, 7, 15, what is the sum of the hash numbers he obtains for the three numbers?
a. 297
b. 273
c. 290
d. 278
Answer: d
Explanation:
As we are subtracting 2 continuously from the resulting numbers, get a progression with a common difference of 2 and we need to multiply the sum by 2 to get hash number.
For example 5: (3 + 1) × 2 = 8
19 : (17 + 15 + 13 + ......+1) × 2 = 81 × 2 = 162
7 : (5 + 3 + 1) × 2 = 18
15: (13 + 11 + 9 + 7 + 5 + 3 + 1) × 2 = 98
Sum of the hash numbers = 278
15. Four people each roll a fair dice once. Find the probability that at least two people will roll the same number?
a. None
b. 5/18
c. 13/18
d. 1295/1296
Answer:
Explanation:
The probability of atleast two persons roll the same number = 1– None of them rolls the same number.
= $1 - \left[ {\dfrac{6}{6} \times \dfrac{5}{6} \times \dfrac{4}{6} \times \dfrac{3}{6}} \right]$ = $1 - \dfrac{5}{{18}} = \dfrac{{13}}{{18}}$